Prof. Dr. Martin Frank
- Director
-
https://calendly.com/martinfrank/office-hour
-
449 (CN), 20.30 (CS)
-
385 (CN), 3.019 (CS)
-
+49 721 608-29267
+49 721 608-48088 -
martin frank ∂does-not-exist.kit edu
Scientific Computing Center
Hermann-von-Helmholtz-Platz 1
76344 Eggenstein-Leopoldshafen
CV
- 09/17 - present: Director Scientific Computing Center (SCC) at KIT and Professor for Computational Science and Mathematical Methods, Department of Mathematics at KIT
- 03/21 - present: Scientific speaker, KIT Graduate School on Computational & Data Science
- 10/18 - 10/23: Scientific Speaker KIT Center Mathematics in Sciences, Engineering, and Economics
-
10/09 - 08/17: Professor at Dept. of Mathematics and Center for Computational Engineering Science, RWTH Aachen University
-
10/08 - 09/09 : Junior professor at Dept. of Mathematics, TU Kaiserslautern
-
10/04 - 09/08 : Research assistant at Dept. of Mathematics, TU Kaiserslautern
-
05/05 : PhD in Mathematics with A. Klar, TU Kaiserslautern
-
10/01 - 09/04 : Research assistant at Dept. of Mathematics, TU Darmstadt
-
04/97 - 02/04 : Studies in Mathematics and Physics, TU Darmstadt
-
02/04 : Diploma in Physics with J. Wambach
-
09/01 : Diploma in Mathematics with R. Farwig
Publications
You can find citation data on my Google Scholar page.
Recent work
- J. Kusch, J. Wolters, M. Frank: Intrusive acceleration strategies for uncertainty quantification for hyperbolic systems of conservation laws, arXiv:1912.09238 [math.NA]
- P. Richter, J. Wolters, R. Cakar, A. Verhoeven-Mrosek, M. Frank: Uncertainty Quantification for Offshore Wind Farms, submitted.
- P. Richter, M. Frank, E. Abraham: Multi-objective optimization of solar tower heliostat fields
Journal publications
- P. Stammer, L. Burigo, O. Jaekel, M. Frank, N. Wahl: Efficient uncertainty quantification for Monte Carlo dose calculations using importance (re-)weighting, to appear in Phys. Med. Biol. (2021).
- T. Xiao, M. Frank: A stochastic kinetic scheme for multi-scale plasma transport with uncertainty quantification, J. Comput. Phys. 432 (2021) 110139.
- Z. Peng, R.G. McClarren, M. Frank: A low-rank method for two-dimensional time-dependent radiation transport calculations, J. Comput. Phys. 421 (2020) 109735.
- S. Simonis, M. Frank, M.J. Krause: On relaxation systems and their relation to discrete velocity Boltzmann models for scalar advection-diffusion equations, Phil. Trans. R. Soc. A 378 (2019) 20190400.
- J. Kusch, R.G. McClarren, M. Frank: Filtered Stochastic Galerkin Methods For Hyperbolic Equations, to appear in J. Comput. Phys.
- G.W. Alldredge, M. Frank, C.D. Hauck: A regularized entropy-based moment method for kinetic equations, to appear in SIAM J. Appl. Math. (2019).
- M.P. Laiu, M. Frank, C.D. Hauck: A Positive Asymptotic Preserving Scheme for Linear Kinetic Transport Equations, SIAM J. Sci. Comput. 41 (2019) A1500–A1526.
- T. Trimborn, L. Pareschi, M. Frank: Portfolio Optimization and Model Predictive Control: A Kinetic Approach, to appear in Discrete Cont. Dyn. B
- J. Kusch, G.W. Alldredge, M. Frank: Maximum-principle-satisfying second-order Intrusive Polynomial Moment scheme, SMAI J. Comput. Math. 5 (2019) 23-51.
- T. Camminady, M. Frank, K. Kuepper, J. Kusch: Ray Effect Mitigation for the Discrete Ordinates Method through Quadrature Rotation, J. Comput. Phys. 382 (2019) 105-123.
- J. Tervo, P. Kokkonen, M. Frank, M. Herty: On Approximative Linear Boltzmann Transport Equation for Charged Particle Transport, Math. Mod. Meth. Appl. Sci. 28 (2018) 2905-2939.
- T. Trimborn, M. Frank, S. Martin: Mean Field Limit of a Behavioral Financial Market Model, Physica A 505 (2018) 613-631.
- P. Chidyagwai, M. Frank, F. Schneider, B. Seibold: A Comparative Study of Limiting Strategies in Discontinuous Galerkin Schemes for the M1 Model of Radiation Transport, J. Comput. Appl. Math. 342 (2018) 399-418.
- M. Frank, C. Lax, S. Walcher, O. Wittich: Quasi-steady state reduction for the Michaelis-Menten reaction-diffusion system, J. Math. Chem. 56 (2018) 1759-1781.
- J. Tervo, P. Kokkonen, M. Frank, M. Herty: On existence of solutions for Boltzmann Continuous Slowing Down transport equation, J. Math. Anal. Appl. 460 (2018) 271-301.
- M. Frank, W. Sun, Fractional Diffusion Limits of Non-Classical Transport Equations, Kinet. Relat. Models 11 (2018) 1503-1526.
- T. Pichard, G.W. Alldredge, S. Brull, B. Dubroca, M. Frank: An approximation of the M 2 closure: application to radiotherapy dose simulation, J. Sci. Comput. 71 (2017) 71-108.
- K. Kuepper, M. Frank, S. Jin: An Asymptotic Preserving 2-D Staggered Grid Method for multiscale transport equations, SIAM J. Numer. Anal. 54 (2016) 440–461.
- P. Otte, M. Frank: Derivation and analysis of Lattice Boltzmann schemes for the linearized Euler equations, Comput. Math. Appl. Volume 72 (2016) 311–327.
- R.C. Barnard, M. Frank, K. Krycki: Sensitivity Analysis for Dose Deposition in Radiotherapy via a Fokker-Planck Model, Math. Med. Biol. (2016).
- M. Frank, C.D. Hauck, K. Kuepper: Convergence of Filtered Spherical Harmonic Equations for Radiation Transport, Commun. Math. Sci. 14 (2016) 1443–1465.
- T. Pichard, G. W. Alldredge, S. Brull, B. Dubroca, M. Frank: The M2 Model for Dose Simulation in Radiation Therapy, J. Comput. Theor. Transp. 45 (2016) 174-183.
- T. Pichard, D. Aregba-Driollet, S. Brull, B. Dubroca, M. Frank: Relaxation schemes for the M1 model with space-dependent flux: application to radiotherapy dose calculation, Commun. Comput. Phys. 19 (2015) 168-191.
- J. Caron, J.-L. Feugeas, B. Dubroca, G. Kantor, C. Dejean, T. Pichard, P. Nicolai, E. D'Humières, M. Frank, V. Tikhonchuk: Deterministic model for the transport of energetic particles. Application in the electron radiotherapy, Physica Medica 31 (2015) 912–921.
- M. Frank, K. Krycki, E.W. Larsen, R. Vasques: The Non-Classical Boltzmann Equation, and Diffusion-Based approximations to the Boltzmann Equation, SIAM J. Appl. Math. 75 (2015) 1329–1345.
- F. Schneider, G. Alldredge, M. Frank, A. Klar: Higher order mixed moment approximations for the Fokker-Planck equation in one space dimension, SIAM J. Appl. Math. 74 (2014) 1087–1114.
- B. Seibold, M. Frank: StaRMAP - A second order staggered grid method for spherical harmonics moment equations of radiative transfer, ACM Trans. Math. Softw. 41 (2014) 4.
- M. Frank, C.D. Hauck, E. Olbrant: Perturbed, Entropy-Based Closure for Radiative Transfer, Kinet. Relat. Models 6 (2013) 557-587.
- E. Olbrant, E.W. Larsen, M. Frank, B. Seibold: Asymptotic Derivation and Numerical Investigation of Time-Dependent Simplified Pn Equations, J. Comput. Phys. 238 (2013) 315-336.
- K. Krycki, C. Berthon, M. Frank, R. Turpault: Asymptotic preserving numerical schemes for a non-classical radiation transport model for atmospheric clouds, Math. Meth. Appl. Sci. 36 (2013) 2101–2116.
- R. Barnard, M. Frank, M. Herty: Optimal radiotherapy treatment planning using minimum entropy models, Appl. Math. Comput. 219 (2012) 2668–2679.
- E. Olbrant, C.D. Hauck, M. Frank: A Realizability-Preserving Discontinuous Galerkin Method for the M1 Model of Radiative Transfer, J. Comput. Phys. 231 (2012) 5612–5639.
- M. Frank, M. Herty, M. Hinze: Time-dependent Closed Loop Control of the Radiative Transfer Equations with Applications in Radiotherapy, Z. Angew. Math. Mech. 92 (2012) 8-24.
- M. Frank, B. Seibold: Optimal Prediction for Radiative Transfer: A New Perspective on Moment Closure, Kinet. Relat. Models 4 (2011) 717-733.
- M. Frank, J. Lang, M. Schäfer: Adaptive Finite Element Simulation of the Time-Dependent Simplified PN Equations, J. Sci. Comput. 49 (2011) 332-350.
- C. Berthon, M. Frank, C. Sarazin, R. Turpault: Numerical methods for balance laws with space dependent flux: application to radiotherapy dose calculation, Commun. Comput. Phys. 10 (2011) 1184-1210.
- M. Schäfer, M. Frank, C.D. Levermore: Diffusive Corrections to Pn approximations, Multiscale Model. Simul. 9 (2011) 1-28.
- M. Frank, A. Klar, R. Pinnau: Optimal Control of Glass Cooling Using Simplified Pn Theory, Transp. Theory Stat. Phys. 39 (2010) 282-311.
- B. Dubroca, J.-L. Feugeas, M. Frank: Angular moment model for the Fokker-Planck equation, Eur. Phys. J. D 60 (2010) 301–307.
- M. Frank, T. Goudon: On a generalized Boltzmann equation for non-classical particle transport, Kinet. Relat. Models 3 (2010) 395-407.
- E. Olbrant, M. Frank: Application of Generalized Fokker-Planck Theory To Electron And Photon Transport In Tissue, Comput. Math. Meth. Med. 11 (2010) 313-339.
- R. Duclous, B. Dubroca, M. Frank: Deterministic Partial Differential Equation Model for Dose Calculation in Electron Radiotherapy, Phys. Med. Biol. 55 (2010) 3843-3857.
- M. Frank, A. Fügenschuh, M. Herty, L. Schewe: The Coolest Path Problem, Netw. Heterog. Media 5 (2010) 143-162.
- M. Frank, M. Herty, A.N. Sandjo: Optimal Radiotherapy Treatment Planning Governed by Kinetic Equations, Math. Mod. Meth. Appl. Sci. 20 (2010) 661-678.
- B. Seibold, M. Frank: Optimal prediction for moment models: crescendo diffusion and reordered equations, Continuum Mech. Thermodyn. 21 (2009) 511-527.
- M. Frank, M. Herty, M. Schäfer: Optimal Treatment Planning in Radiotherapy Based On Boltzmann Transport Calculations, Math. Mod. Meth. Appl. Sci. 18 (2008) 573-592.
- M. Frank, A. Klar, E.W. Larsen, S. Yasuda: Time-dependent Simplified PN Approximation to the Equations of Radiative Transfer, J. Comput. Phys. 226 (2007) 2289-2305.
- M. Frank: Approximate models for radiative transfer, Bull. Inst. Math. Acad. Sinica (New Series) 2 (2007) 409-432.
- M. Frank, H. Hensel, A. Klar: A fast and accurate moment method for the Fokker-Planck equation and applications to electron radiotherapy, SIAM J. Appl. Math. 67 (2007) 582-603.
- M. Frank, R. Pinnau: Existence and Bounds for the Half Moment Entropy Approximation to Radiative Transfer, Appl. Math. Lett. 20 (2007) 189-193.
- M. Frank, B. Dubroca, A. Klar: Partial Moment Entropy Approximation to Radiative Heat Transfer, J. Comput. Phys. 218 (2006) 1-18.
- M. Schäfer, M. Frank, R. Pinnau: A Hierarchy of Approximations to the Radiative Heat Transfer Equations: Modelling, Analysis and Simulation, Math. Mod. Meth. Appl. Sci. 15 (2005) 643-665.
- R. Turpault, M. Frank, B. Dubroca, A. Klar: Multigroup half space moment appproximations to the radiative heat transfer equations, J. Comput. Phys. 198 (2004) 363-371.
- M. Seaid, M. Frank, A. Klar, R. Pinnau, G. Thömmes: Efficient numerical methods for radiation in gas turbines, J. Comput. Appl. Math. 170 (2004) 217-239.
- M. Frank, M. Seaid, J. Janicka, A. Klar, R. Pinnau: A comparison of approximate models for radiation in gas turbines, Progress in Computational Fluid Dynamics 4 (2004) 191-197.
- M. Frank, M. Buballa, M. Oertel: Flavor-mixing effects on the QCD phase diagram at non-vanishing isospin chemical potential: one or two phase transitions?, Phys. Lett. B 562 (2003) 221-226.
- B. Dubroca, M. Frank, A. Klar, G. Thömmes: A half space moment approximation to the radiative heat transfer equations, Z. Angew. Math. Mech. 83 (2003) 853-858.
Mathematics Education
- S. Schönbrodt, T. Camminady, M. Frank: Mathematische Grundlagen der künstlichen Intelligenz im Schulunterricht, Math. Semesterber. (2021) doi.org/10.1007/s00591-021-00310-x
- M. Sube, T. Camminady. M. Frank, C. Roeckerath: Vorschlag für eine Abiturprüfungsaufgabe mit authentischem und relevantem Realitätsbezug. In: Greefrath G., Maaß K. (eds) Modellierungskompetenzen – Diagnose und Bewertung. Realitätsbezüge im Mathematikunterricht. Springer Spektrum, Berlin, Heidelberg (2020).
- M. Frank, C. Roeckerath: Augmenting Mathematics Courses by Problem-Based Learning, International Journal of Engineering Pedagogy (iJEP) 6 (2016), doi:10.3991/ijep.v6i1.5368
- M. Frank, M. Hattebuhr, C. Roeckerath: Augmenting Mathematics Courses by Project-Based Learning, Proceedings of 2015 International Conference on Interactive Collaborative Learning (2015).
- M. Frank, C. Roeckerath: Wie kann man mit einer Handykamera Geschwindigkeiten messen?, Der Mathematikunterricht 61 (2015) 27-31.
- M. Frank, C. Roeckerath: Habe ich das Zeug zum MINT-Studium? Die CAMMP week als Orientierungshilfe für Schülerinnen und Schüler, in: Lehren und Lernen von Mathematik in der Studieneingangsphase, Springer-Verlag (2015) 181-195.
- M. Frank, C. Roeckerath: Gemeinsam mit Profis reale Probleme lösen, Mathematik Lehren 174 (2012).
Refereed Proceedings
-
M. Berghoff, M. Frank, B. Seibold: Massively Parallel Stencil Strategies for Radiation Transport Moment Model Simulations. In: Krzhizhanovskaya V. et al. (eds) Computational Science – ICCS 2020. ICCS 2020. Lecture Notes in Computer Science, vol 12143.
-
P. Richter, J. Tinnes, P. Schwarzbözl, A. Rong, M. Frank: Efficient Ray-Tracing with Real Weather Data, to appear in AIP Conference Proceedings (2018).
-
P. Richter, G. Heiming, N. Lukas, M. Frank: SunFlower: A New Solar Tower Simulation Method For Use in Field Layout Optimization, to appear in AIP Conference Proceedings (2018).
-
C.-A. Domínguez-Bravo, S.-J. Bode, G. Heiming, P. Richter, E. Carrizosa, E. Fernández-Cara, M. Frank, P. Gauché: Field-design optimization with triangular heliostat pods, AIP Conference Proceedings 1734 (2016) 070006.
-
R. Barnard, M. Frank, M. Herty: Treatment Planning Optimization for Radiotherapy, Proc. Appl. Math. Mech. 13 (2013) 339–340.
-
R. Barnard, M. Frank, M. Herty: State-Constrained Optimization of PDEs via Infinite Penalization Methods, Proc. Appl. Math. Mech. 12 (2012) 691–692.
- K. Krycki, M. Frank: Numerical treatment of a non-classical transport equation modelling radiative transfer in atmospheric clouds, Hyperbolic Problems: Theory, Numerics and Applications, Series in Contemporary Applied Mathematics 17&18 (2012) 502-509.
- B. Dubroca, M. Frank: An Iterative Method for Transport Equations in Radiotherapy, Progress in Industrial Mathematics at ECMI 2008 (2010) 407-412.
- M. Frank, M. Herty: Boundary control of radiative transfer equations for application in radiotherapy planning, Progress in Industrial Mathematics at ECMI 2008 (2010) 413-418.
- D. Wright, M. Frank, A. Klar: The minimum entropy approximation to the radiative transfer equation, Proc. Symp. Appl. Math. 67 (2009) 987-996.
- M. Frank, H. Hensel, A. Klar: Toward fast and accurate methods for dose calculation in radiotherapy, Proc. Appl. Math. Mech. 7 (2007) 200700407-200700408.
- M. Schäfer, M. Frank, M. Herty: Optimal treatment planning in radiotherapy based on Boltzmann transport calculations, Proc. Appl. Math. Mech. 7 (2007) 2060027-2060028.
- M. Frank, H. Hensel, A. Klar: Toward fast and accurate deterministic methods for dose calculation in electron radiotherapy, IMECS 2007, 2361-2365.
- M. Schäfer, M. Frank, R. Pinnau: Partial Space Moment Approximation for Radiative Transfer, Proc. Appl. Math. Mech. 6 (2006) 761-762.
- M. Frank: Partial Moment Entropy Approximation to Radiative Heat Transfer, Proc. Appl. Math. Mech. 5 (2005) 659-660.
Contributions to Books
- R. Barnard, M. Frank, M. Herty: Optimal Treatment Planning in Radiotherapy Based on Boltzmann Transport Equations, in Trends in PDE Constrained Optimization, International Series of Numerical Mathematics, G. Leugering (et al.) (Eds.), Birkhäuser, 2014.
- M. Frank, K. Küpper, B. Seibold: StaRMAP - A second order staggered grid method for radiative transfer: Application in radiotherapy, in Advances In PDE Modeling and Computation, S. Sundar (ed.), Ane Books, 2014.
- M. Frank, A. Klar: Radiative Heat Transfer and Applications for Glass Production Processes, in Mathematical Models in the Manufacturing of Glass, Lecture Notes in Mathematics, A. Fasano (Ed.), Springer, 2011.
Theses
- M. Frank: Partial Moment Models for Radiative Transfer, Dissertation, Fachbereich Mathematik, TU Kaiserslautern, Shaker-Verlag, Aachen, July 2005.
- M. Frank: Das QCD-Phasendiagramm bei endlicher Isospindichte, Diplomarbeit, Fachbereich Physik, TU Darmstadt, July 2003.
- M. Frank: Stabilitätsanalyse einer gewöhnlichen Differentialgleichung mit zeitabhängiger Retardierung, Diplomarbeit, Fachbereich Mathematik, TU Darmstadt and Robert Bosch GmbH, Schwieberdingen, September 2001.
Projects
Our method-oriented research focuses on:
-
Approximate models for kinetic equations, especially moment models
-
Optimization with partial differential equations and uncertainty quantification
These techniques are applied to several application areas. Furthermore, in interdisciplinary projects the group acts as a bridge to transfer advanced mathematical techniques to real-world problems. Examples include:
-
Dose calculation and treatment plan optimization in radiotherapy
-
Simulation of oxygenation in tumor tissue
-
Photon transport in clouds
-
Steam simulation in solar thermal power plants
-
Crime modeling and traffic flow
-
Time-dependent neutron transport
-
Uncertainty quantification in neutron transport cross sections
Detailed descriptions of selected projects are given below. Student projects can be found here.
Non-destructive elemental analysis of raw materials and contaminated sites - ZEBRA
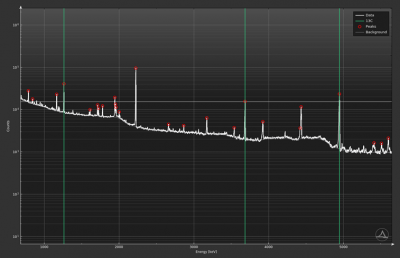
Within the ZEBRA research project, an innovative measurement system is being developed for environmental and hazardous substance analysis. This measurement system is based on the prompt and delayed gamma neutron activation analysis (P&DGNAA). The project includes the construction and test operation of the measurement system and the development of new analytical methods for determining the mass fractions of all elements of the periodic system.
More information: ZEBRA
![]()
Simulating Heavy Ion Beams Numerically using Minimum Entropy Reconstructions - SHINE
The aim of this project is to develop a novel tool for the simulation of heavy ion beams as they are decelerated in thick targets. We want to characterize the spatial and energy distributions of all primary particles and secondary fragments in a target. This is relevant because ion beams are used in various fields: atomic physics (e.g. atomic collisions, ion capture), nuclear physics (e.g. the study of the structure of nuclei), electronics (e.g. deposition of elements), material science and chemistry (e.g. analysis of damage on the walls of a tokamak), biology (e.g. the study of the toxicology of cellular tissues by ion analysis). Additionally, several world-class facilities are dedicated to these studies (e.g. FAIR in Germany, GANIL in France). Simulations of heavy ion beams are challenging for two main reasons. First, beams are difficult to capture with a grid-based method. Second, the simulations rely on measurements of the stopping power, and therefore must be regarded as uncertain. We therefore develop a new entropy-based discretization scheme which allows both a sub-grid resolution and at the same time a very detailed reconstruction that can capture beams. In addition, we will use a similar method to characterize the uncertainties in the particle distribution due to uncertain stopping powers. The method is computationally challenging but highly parallelizable, and therefore ideally suited for modern computer architectures.
More information: SHINE
Moment Models for Radiative Transfer
Developing simplified methods for the simulation of radiative transfer requires taking into account the physical situation that will be analyzed. There are two important limits: optically thick and optically thin media. The different regimes can be characterized by the mean free paths for scattering and for absorption. One problem in this characterization is, that many materials are optically thick in a specific frequency range and optically thin in other ranges. Additionally, there is a transition regime between the two. For instance, during the reentry of a space craft into the atmosphere the regime goes from optically thin (space) through a transition (higher atmosphere) into optically thick (lower atmosphere).
Methods that work well in optically thin media are computationally too expensive in these regimes. Methods that work well in optically thick media, on the other hand, give poor results for low order approximations and have high computational costs if one increases the order. Therefore, in these regimes new methods have to be developed.
These new approximations have to recover traditional reduced models for small mean free paths. Further, in the transition regime, they have to be more accurate than the simplified models and should be solvable more efficiently than the full kinetic approaches.
The field of use for transition regime models can be found in stand-alone solvers for problems that lie completely within the optically thick and transition regime. For problems where the order of the mean free path also covers the optically thin regime, the new approaches could be used in hybrid methods.
Deterministic Methods for Dose Calculation in Radiotherapy
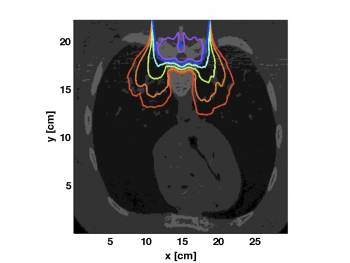
High energy ionizing radiation is a prominent modality for the treatment of many cancers. The approaches to dose calculation can be categorized into semi-empirical models (e.g. Fermi-Eyges, convolution-superposition) and probabilistic methods (e.g. Monte Carlo). A third way to dose calculation has only recently attracted attention in the medical physics community. This approach is based on the deterministic kinetic equations of radiative transfer. In this project, we investigate macroscopic partial differential equation models for particle transport in tissue. The models reduce computational cost, and at the same time preserve key properties of the mesoscopic equation.
The figures show the isodose curves in the case where the vertebral column is irradiatied by 12 MeV electrons. The first figure shows the results obtained with the PenEasy2009 benchmark code, the second figure the results obtained with the reduced model.
Optimal Treatment Planning in Radiotherapy based on Boltzmann Transport Equations
We study optimal control problems modelling clinical external beam radiotherapy. We use the Boltzmann transport equations to model the distribution of radiation through the body. Mathematically, this consists of an integro-partial differential equation which depends on variables in space, energy, and angular direction. Several avenues of investigation are followed. Objective functions which accurately model the response of tumor cells to dose distributions while also describing the clinical requirements for an effective treatment plan will be developed. With these new models, the existence and regularity of the corresponding optimal treatment plans will be studied. Additionally, we pursue the use of moment approximations to the high-dimensional phase space to create efficient numerical schemes for the solution of the optimization problem; the relationship between these approximations and the optimization methods employed will be investigated. Closed-loop control schemes for use in time-dependent 4D radiotherapy will also be developed. Optimal treatment plans will be simulated on real CT-patient data and compared with standard Monte-Carlo methods for the solution of control problems.
Dose Visualization in 3D
Dose distributions in the body are genuinely three-dimensional. Most of the time, they are visualized by two-dimensional slices. In order to compare standard dose calculation results with newly developed deterministic methods, and as a didactical means to explain these new methods, three-dimensional visualizations have been developed in collaboration with the VR group at RWTH Aachen University. Results can be viewed both on desktop computers and on the VR system at AICES. Future developments include the visualization of an optimization process using adjoint information. Data courtesy of the National Library of Medicine Visible Human Project.
Nonclassical Transport in Clouds
In classical particle transport, the probability that a particle interacts with the background medium is proportional to the path length traveled by that particle, and the proportionality constant depends on the density of the medium and on the particle’s energy. This typically leads to an exponential attenuation law, i.e. the particle flux decreases as an exponential function of the path length (Beer-Lambert law). In cloud physics, however, recent experimental studies point toward a non-exponential attenuation law. It has been suggested that spatial correlations between the water droplets (scattering centers) within a cloud could be responsible for this behavior. This hypothesis has sparked a vivid discussion in the recent literature.
In this project, we investigate a nonclassical Boltzmann equation proposed by Larsen. We have rigorously established the convergence of the solution in the diffusion limit. We will develop numerical schemes for the efficient solution of the extended Boltzmann model.
Direct Steam Simulation in Solar Thermal Power Plants
Concentrated solar power systems are systems that use mirrors to concentrate sunlight to heat a fluid. The heated fluid is converted into steam which drives a turbine to generate electrical power.
There exist different types of concentrators. For example, Fresnel reflectors (see figure) are made of many thin, flat mirror strips that concentrate sunlight onto tubes through which a working fluid is pumped. The idea of direct steam generation is to use water as the working fluid.
In this project we consider the flow of water inside an absorber tube. This two-phase flow is modeled as a homogeneous flow. Specifically, the flow is governed by the 1D Euler equations. The influence of solar energy is described by a heat equation which is coupled with the flow. Due to a specific closure relation for the two-phase flow, the system is in a non-conservative form. We will develop a model and numerical schemes to simulate the flow through a realistic network of tubes.
Neutron Imaging System for Radioactive Waste Analysis
Similar to x-rays, neutrons can be used for imaging. The advantage of fast neutrons with respect to x-rays is their deeper penetration depth into dense materials. This project deals with the development of a compact neutron radiography system, which can be used in addition to existing imaging techniques. The main aplication is the characterization of radioactive waste, but the technology can be used e.g. for electronics recycling, quality control in manufacturing, engine design, among others. In a collaborative project, we develop image reconstruction algorithms based on the radiative transfer equation. The main focus is the correction of diverging beams.
Extinction Photometry for the Characterization of a Multi-Component Aerosol
This project aims at improving measurement techniques for the characterization of the composition of an aerosol. The main goal is to implement, adapt and improve the method of Mie inversion so that physically correct particle size distributions can be obtained from measured spectra automatically without an operator.
Analysis and Numerics of Kinetic-Continuum Coupling
In numerical methods for engineering applications, there are three basic methods which can be applied: either we work with continuum equations (macroscopic level), or with individual particles (microscopic), or as a third approach we use a probability density for the distribution of the particles for which we solve solve a PDE (mesoscopic). Each of the three has its advantages and disadvantages, therefore our approach is to couple them such that in each part of the simulation domain, we apply the best-suited methodology. This requires special analysis of the coupling method itself. Typically this is based on asymptotic approaches which under given restrictions / assumptions tend to the desired set of equations on the other side of the coupling interface. These assumptions have to be matched with the properties of the numerical schemes. Special focus will be put on the coupling of the Lattice Boltzmann method with linearized Euler equations for aero-acoustic simulation.
| Titel | Typ | Semester | Ort |
|---|---|---|---|
| Uncertainty Quantification | Vorlesung (V) | SS 2019 | |
| Oberseminar Computational Science and Mathematical Methods | Seminar (S) | SS 2019 | |
| Advanced Topics in Parallel Computing | Seminar (S) | SS 2019 |
Older Lectures and Seminars
- Uncertainty Quantification, KIT, summer term 2018
- Seminar Computational Science and Mathematical Methods, KIT, summer term 2018
- Introduction to Transport Theory, KIT, winter term 2017/18
- Seminar Computational Science and Mathematical Methods, KIT, winter term 2017/18
- Numerical Analysis II, RWTH Aachen, summer term 2017
- Mathematics IV (CES), RWTH Aachen, summer term 2017
- Introduction to Transport Theory, RWTH Aachen, summer term 2017
- Numerical Analysis I, RWTH Aachen, winter term 2016/17
- Mathematics III (CES), RWTH Aachen, winter term 2016/17
- Uncertainty Quantification, RWTH Aachen, winter term 2016/17
- Partial Differential Equations (CES), RWTH Aachen, winter term 2015/16
- Seminar Asymptotic-Preserving Numerical Schemes, RWTH Aachen, winter term 2015/16
- Mathematics IV (CES), RWTH Aachen, summer term 2015
- Computational and Statistical Inverse Problems, RWTH Aachen, summer term 2015
- Mathematics III (CES), RWTH Aachen, winter term 2014/15
- Computational Nuclear Engineering, RWTH Aachen, winter term 2014/15
- Seminar Hydrodynamic Limits of the Boltzmann Equation, RWTH Aachen, winter term 2014/15
- Mathematics II (CES), RWTH Aachen, summer term 2014
- Uncertainty Quantification, RWTH Aachen, summer term 2014
- Partial Differential Equations (CES), RWTH Aachen, winter term 2013/14
- Computational Nuclear Engineering, RWTH Aachen, winter term 2013/14
- Mathematics IV (CES), RWTH Aachen, summer term 2013
- Introduction to Transport Theory, RWTH Aachen, summer term 2013
- Mathematics III (CES), RWTH Aachen, winter term 2012/13
- Uncertainty Quantification, RWTH Aachen, winter term 2012/13
- Computational Nuclear Engineering, RWTH Aachen, winter term 2012/13
- Mathematics III (CES), RWTH Aachen, winter term 2011/12
- Computational Nuclear Engineering, RWTH Aachen, winter term 2011/12
- Seminar on Nonsmooth Analysis & Applied Optimization, RWTH Aachen, winter term 2011/12
- Mathematics IV (CES), RWTH Aachen, summer term 2011
- Introduction to Transport Theory, RWTH Aachen, summer term 2011
- Seminar on Ordinary Differential Equations, RWTH Aachen, summer term 2011
- Mathematics III (CES), RWTH Aachen, winter term 2010/11
- Partial Differential Equations (CES), RWTH Aachen, winter term 2010/11
- Mathematics II (CES), RWTH Aachen, summer term 2010
- Mathematics IV (CES), RWTH Aachen, summer term 2010
- Introduction to Transport Theory, RWTH Aachen, summer term 2010
- Mathematics I (CES), RWTH Aachen, winter term 2009/10
- Mathematics III (CES), RWTH Aachen, winter term 2009/10
- Introduction to Numerical Mathematics, TU Kaiserslautern, winter term 2008/09
- Mathematics III for Engineers, TU Kaiserslautern, winter term 2008/09
- Mathematics II for Engineers, TU Kaiserslautern, winter term 2007/08
- Mathematics I for Engineers, TU Kaiserslautern, summer term 2007
- Proseminar Fractal Geometry, TU Kaiserslautern, winter term 2005/06
- Seminar Partial Differential Equations, TU Kaiserslautern, winter term 2005/06
Modeling Projects
-
CAMMP Modeling Week in Aachen, RWTH Aachen, September 2017
-
CAMMP Modeling Week in Voeren, RWTH Aachen, June 2017
-
CAMMP Modeling Week in Aachen, RWTH Aachen, September 2016
-
CAMMP Modeling Week in Voeren, RWTH Aachen, June 2016
-
CAMMP Modeling Week in Aachen, RWTH Aachen, September 2015
-
CAMMP Modeling Week in Voeren, RWTH Aachen, June 2015
-
CAMMP Modeling Week in Aachen, RWTH Aachen, September 2014
-
CAMMP Modeling Week in Voeren, RWTH Aachen, June 2014
-
CAMMP Modeling Week in Aachen, RWTH Aachen, November 2014
-
CAMMP Modeling Week in Voeren, RWTH Aachen, July 2013
-
CAMMP Modeling Week in Voeren, RWTH Aachen, July 2012
-
CAMMP Modeling Week in Nideggen, RWTH Aachen, May 2011
-
ECMI Modeling Week in Rouen, France, TU Kaiserslautern, August 2007
-
Modeling Week in Lambrecht, TU Kaiserslautern, July 2005
-
Modeling Week in Termeno, Italy, TU Kaiserslautern, March 2005
-
Proseminar Mathematical Modeling, TU Kaiserslautern, winter term 2004/05
-
Proseminar I - Mathematical Modeling, TU Darmstadt, winter term 2003/04
-
Modeling Week in Fuldatal, TU Darmstadt, September/October 2003
-
Seminar on Mathematical Modeling, TU Darmstadt, winter term 2002/03
-
Modeling Week in Hoechst, TU Darmstadt, September/October 2002
CAMMP (Computational and Mathematical Modeling Program)
Modeling projects are ideal ways to teach problem solving capabilities. Students are faced with a real-world problem that is not formulated in the language of Mathematics. In order to translate the problem, it is neccessary to read literature from other disciplines. Each group of students learns Mathematics by doing it. The project aims can be adapted to the group’s capabilities so that weaker students gain motivation by solving easier problems, while stronger students can be challenged by more complicated additional questions. Problem-solving skills can be assessed by industrial case studies in the final year. The students are confronted with a real problem, have to do research, have to work in a team and in the end have to present their results in a comprehensible way. To facilitate problem-based learning, I have co-founded the education lab CAMMP (Computational and Mathematical Modeling Program) at RWTH Aachen. Our activities in Karlsruhe can be found here.
Students
I have advised or co-advised the following PhD students, in chronological order of graduation:
- Edgar Olbrant: Models and Numerical Methods for Time- and Energy-Dependent Particle Transport, 2012
- Philipp Monreal: Moment Realizability and Kershaw Closures in Radiative Transfer, 2012
- Kai Krycki: Mathematical Modeling and Numerical Methods for Non-classical Transport in Correlated Media, 2015
- Kerstin Küpper: Numerical Methods, and Uncertainty Quantification for Radiation Therapy, 2016
- Bahodir Ahmedov: Approximation Methods and Reduced Models for Optimal Radiation Treatment, 2016
- Teddy Pichard: Mathematical modelling for dose deposition in photontherapy, 2016
- Pascal Richter: Mathematical Models and Methods for Solar Tower Power Plants, 2017
- Tobias Kyrion: New Algorithms for Mie Inversion, 2017
- Torsten Trimborn: Kinetic Modeling of Financial Market Models, 2018
- Philipp Otte: Analysis, numerics, and implementation of kinetic-continuum coupling using Lattice-Boltzmann methods, 2018
- Maike Sube: Entwicklung und Evaluation von Unterrichtsmaterial zu Data Science und mathematischer Modellierung mit Schülerinnen und Schülern, 2019
- Jonas Kusch: Realizability-preserving discretization strategies for hyperbolic and kinetic equations with uncertainty, 2020
- Thomas Camminady: Theory, models, and numerical methods for classical and non-classical transport, 2021
- Kirsten Wohak: Didaktisch-methodische Entwicklung und Evaluation von computergestützten Lehr- und Lernmaterialien zur Mathematik inverser Probleme, 2021
- Maren Hattebuhr: Methodisch-didaktische Entwicklung und Evaluation von interaktiven Lehr- und Lernmaterialien zur Mathematik im Bereich der Klimaforschung, 2021
- Sarah Schönbrodt: Optimierungsprobleme in der mathematischen Modellierung, 2022
- Pia Stammer: Uncertainty quantification and numerical methods in charged particle radiation therapy, 2023
- Steffen Schotthöfer: Synergies between Numerical Methods for Kinetic Equations and Neural Networks, 2023
- Gayatri Caklovic: ParaDiag and Collocation Methods: Theory and Implementation, 2023
I have advised or co-advised the following postdocs, in chronological order:
- Richard Barnard
- Richard Vasques
- Graham Alldredge
- Pascal Richter
- Jonas Kusch
- Tianbai Xiao
- Sarah Schönbrodt

